백준 1167번 JAVA

https://www.acmicpc.net/problem/1167

1167번: 트리의 지름

import java.util.*;
 
public class Main {    
 
    static ArrayList<Node>[] list;  //트리의 두 정점을 잇기 위한 ArrayList 데이터 타입은 Node 객체
    static boolean[] visited;  //노드 방문여부를 위한 boolean배열
    static int max = 0;  // 그 정점까지의 거리 초기화
    static int node;  
    
    public static void main(String args[]) {
        Scanner scan = new Scanner(System.in);  
        
        int n = scan.nextInt();  //먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고
        list = new ArrayList[n + 1]; //정점의 개수만큼 ArrayList크기설정
        for(int i = 1; i < n + 1; i++) {
            list[i] = new ArrayList<>();  ////정점의 개수만큼 ArrayList크기설정
        } 
        
        for(int i = 0; i < n; i++) {
            int s = scan.nextInt();  //정점 번호1
            while(true) {
                int e = scan.nextInt(); //정점 번호2
                if(e == -1) break;
                int cost = scan.nextInt();  //정점 번호1에서 정점번호2까지의 거리
                list[s].add(new Node(e, cost));  //list[s]정점번호1 new Node(e, cost) e 정점번호2 cost 정점번호 1에서2까지의 거리
            }
        }
        
        //임의의 노드(1)에서 부터 가장 먼 노드를 찾는다. 이때 찾은 노드를 node에 저장한다.
        visited = new boolean[n + 1];
        dfs(1, 0);
        
        //node에서 부터 가장 먼 노트까지의 거리를 구한다.
        visited = new boolean[n + 1];
        dfs(node, 0);
        
        System.out.println(max);
    }
    
    public static void dfs(int x, int len) {  //x노드 len 거리
        if(len > max) {  //기존에 있는 노드정점간의 거리(max)보다 현재 노드간의 정점의 거리가 더 길면
            max = len;  //현재 노드의 길이를 max에 저장하고
            node = x;  //노드의 정점 
        }
        visited[x] = true;
        
        for(int i = 0; i < list[x].size(); i++) { //list[x].size()만큼 반복
            Node n = list[x].get(i);  //현재 정점 번호와 인접한 정점번호 그 정점까지의 거리정보를 가지고 있는 node
            if(visited[n.e] == false) {  //다른 정점 번호를 방문하지 않았다면
                dfs(n.e, n.cost + len);  //다른 정점번호를 현재정점 번호로 바꿔주고 정점까지의 거리를 누적시킨다
                visited[n.e] = true;  //방문 체크
            }
        }
        
    }
    
    public static class Node {
        int e;
        int cost;
        
        public Node(int e, int cost) {
            this.e = e;
            this.cost = cost;
        }
    }
}

 트리에서 가장 먼 정점 사이의 거리를 구하는 문제이다. 정점의 위치 보다는 정점과 정점 사이의 cost값이 중요하다. 

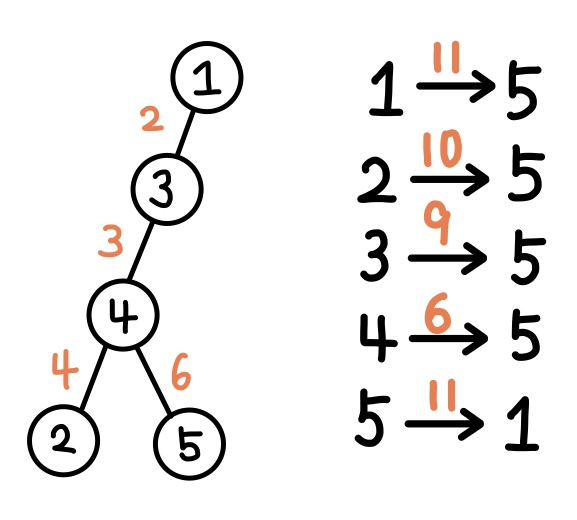
각 정점에서 제일 먼 정점 까지의 거리를 구해보면 오른쪽에 적힌 값과 같다.

이때 트리에서 가장 먼 정점 사이의 거리는 1 <-> 5 인 11이다.

 

그림을 보면 공통점이 보인다. 5 -> 1, 1 -> 5가 가장 먼 정점 사이의 거리일때 모든 정점에서 부터의 최장 정점은 1 또는 5를 항상 포함하고 있다.

 

또한 한 정점에서 가장 먼 정점으로 가는 경로와 가장 먼 정점 사이의 경로는 항상 일부가 겹친다. 아래 그래프를 보면서 이해해보자.

같은 그래프를 최장 거리를 가진 정점을 기준으로 표현하면 왼쪽과 같은 그림이 된다. 주황색으로 표시된 경로가 최장 경로가 된다.

 

이때 각 정점에서 제일 멀리있는 정점 까지 가는 길을 따라가 보면 항상 일부가 겹치는 것을 알 수 있다. 정점간 cost를 기준으로 경로를 결정하기 때문에 가장 긴 정점의 경로는 결국 어느 정점에서의 가장 먼 거리에 있는 정점의 경로와 겹칠 수밖에 없는 것이다. 

 

그렇기 때문에 모든 정점에서 부터의 최장 정점은 항상 가장 먼 정점인 1이나 5를 포함할 수 밖에 없다.

이에 대한 반례로, 만약 4에서 최장 정점이 2가 되려면 그 cost가 11보다 큰 값으로 변경되어야 한다. 이렇게 되면 가장 먼 정점 또한 2를 포함하도록 변경되는 것을 알 수 있다.

 

위에서 구했듯이 각 정점에서 최장 정점을 구하면 항상 가장 먼 정점 중 하나를 포함하는 것을 알 수 있다. 그럼 이제 그 정점에서 가장 먼 정점을 구하면된다. 1이 구해졌다면 1에서 가장 먼 정점인 5가 될 것이고, 5가 구해졌다면 가장 먼 정점인 1이 될 것이다.

즉, 다음과 같은 과정이 필요하다.

1. dfs를 통해 임의의 정점 하나에서 가장 먼 정점을 구한다. (임의의 정점은 아무거나 상관없다.)

2. dfs를 통해 구한 정점으로 부터 가장 먼 정점까지의 거리를 구한다.